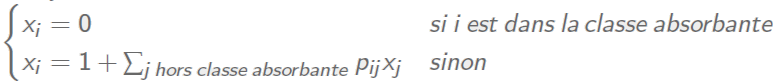Contents
ToggleAbsorption of a state
A markov chain is absorbing (absorption of a state) if and only if: there is at least one absorbing state, from any non-absorbing state, one can reach an absorbing state. For any absorbing Markov chain and for any starting state, the probability of being in an absorbing state at time t tends to 1 when t tends to infinity.
When dealing with an absorbing Markov chain, we are generally interested in the following two questions:
- How long will it take on average to arrive in an absorbent state, given its initial state?
- If there are several absorbing states, what is the probability of falling into a given absorbing state?
If a Markov chain is absorbent, we will place the absorbing states at the beginning; we
will then have a transition matrix of the following form (I is a unit matrix and 0
a matrix of 0):

The matrix N = (IQ)-1 is called the fundamental matrix of the absorbent chain. Consider the following stochastic matrix:

We then have to calculate N:
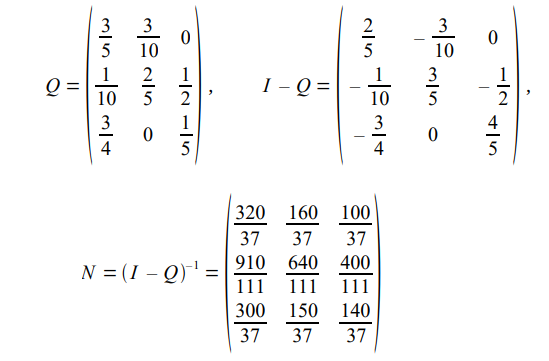
The average number of steps before absorption knowing that we start from state i (not
absorbent) is the sum of the terms of the i-th row of N.
In the previous example, the average number of steps before absorption is taken from the first line, starting from state 1: 320/37 + 160/37 + 100/37 = 15.67.
In the same example:
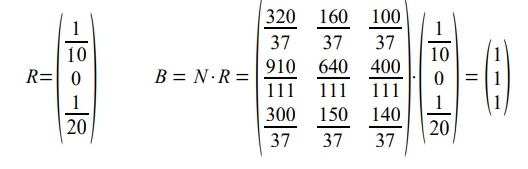
The probability of being absorbed by the unique absorbing state is 1 whatever the initial state!
Linear equations
From a linear equation point of view, the vector of absorption probabilities is the smallest positive solution of the system:

The vector of mean time to reach is the smallest positive solution of the system: