Contenido
PalancaCodificación Huffman
La codificación Huffman es un método ampliamente utilizado en la compresión de datos. Se utiliza para codificar un texto en binario, utilizando para cada letra un número de bits en función del número de veces que aparece la letra: cuanto más aparece la letra, menor es el número de bits. Por lo tanto, el número total de bits utilizados para codificar el texto se reduce en comparación con la codificación ASCII estándar que utiliza ocho bits para cada letra.
Cuando se trata de transmitir información en un canal no ruidoso, el objetivo prioritario es minimizar el tamaño de la representación de la información: este es el problema de la compresión de datos. El código de Huffman (1952) es un código óptimo de longitud variable, es decir tal que la longitud media de un texto codificado es mínima. Se observan así reducciones de tamaño del orden de 20 a 90%.
El código binario asociado con cada letra está definido por un árbol binario. Las hojas del árbol corresponden a las letras del alfabeto. Los nodos internos no contienen información. El camino tomado para llegar a una hoja desde la raíz define el código de la letra en esta hoja: izquierda 0, derecha 1. Por ejemplo:
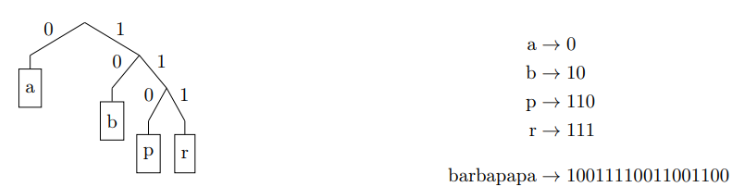
árbol de huffman
Cuando se conoce el texto a codificar, es posible optimizar el árbol binario utilizado para acortar los códigos de las letras más frecuentes. Esto es lo que hace el algoritmo de Huffman: comienza contando el número de ocurrencias de cada carácter en el texto. Por ejemplo, en la oración:

A partir de estas frecuencias, el algoritmo inicializa un árbol por carácter, teniendo como peso el número de apariciones del carácter:

En cada iteración, el algoritmo selecciona los dos árboles con los pesos más bajos y los ensambla para formar los dos hijos de un árbol binario cuyo peso es la suma de los dos árboles. Cuando se atan varios árboles por el menor peso, el árbol seleccionado entre ellos puede ser cualquiera. Así, en la primera iteración, podríamos obtener:

y después de cuatro iteraciones más:

Cuando solo queda un árbol, el algoritmo ha terminado.
Aquí hay un ejemplo de construcción del árbol de Huffman para comprender mejor el proceso. En este ejemplo hemos colocado las letras en orden ascendente a diferencia del ejemplo anterior:

algoritmo de Huffman
Más formalmente, el algoritmo de Huffman es el siguiente:

Codificación y decodificación
Podemos reescribir el árbol en forma de matriz. La codificación de una letra está ligada al camino recorrido en el árbol hasta la letra deseada. Tome la siguiente tabla:

Este tipo de código se dice prefijo, lo que significa que ningún código es el prefijo de otro (el código de A es 10 y ningún otro código comienza con 10, el código de B es 001 y ningún otro código no comienza con 001 ). Esta propiedad permite que los caracteres se separen sin ambigüedades.
Atención, aquí todo lleva a creer que la tabla propuesta no es la óptima. De hecho, hay 8 caracteres, por lo que usando binario, podríamos usar 3 bits para codificar todos los caracteres (2^3 = 8 posibilidades).
Aquí, la suma de los bits de letras codificados es 2+3+3+4+2+4+4+4 = 26 bits, o un promedio de 26/8 = 3,25 bits por carácter. Pero en realidad lo que contará no es la media, sino la media ponderada en frecuencia como veremos en el ejercicio de ejemplo.
Usando la matriz, es posible codificar un mensaje (aquí el + es una concatenación):
CACHE=000+10+000+1111+01=00010000111101.
Por tanto, tenemos un mensaje de 14 bits en lugar de 5*3=15 bits, lo que corresponde a una reducción de memoria para el almacenamiento de texto de (15-14)/15 = 6,61 TP2T. Aunque en promedio la codificación es más grande, ¡de hecho tenemos una reducción en el espacio de memoria utilizado!
Ejemplo
1) Buscamos codificar cada letra de este alfabeto mediante una secuencia de dígitos binarios.
a) Cuantos bits se necesitan para codificar cada una de las 8 letras del alfabeto.
b) ¿Cuál es la longitud en bytes de un mensaje de 1000 caracteres basado en este alfabeto?
2) Proporcione un código de tamaño fijo para cada carácter del alfabeto de 8 letras.
3) Consideremos ahora la siguiente codificación, siendo variable la longitud del código de cada carácter.

a) Utilizando la tabla anterior, dar el código de mensaje: CACHE.
b) Cuál es el mensaje correspondiente al código 001101100111001.
4) En un texto, cada uno de los 8 caracteres tiene un número diferente de ocurrencias. Esto se resume en la siguiente tabla, construida a partir de texto de 1000 caracteres.

a) Usando el código de tamaño fijo propuesto en la pregunta 2, ¿cuál es la longitud en bits del mensaje que contiene los 1000 caracteres enumerados en la tabla anterior?
b) Usando el código de la pregunta 3, ¿cuál es la longitud del mismo mensaje en bits?
5) Realiza el árbol de Huffman optimizando el espacio de memoria. Vuelva a hacer las preguntas 3 y 4 con el nuevo árbol.
Corrección del ejemplo
1a – Para codificar las 8 letras se necesitan 3 bits porque 23 = 8.
1b – 1000 caracteres corresponden a 1000*3 = 3000 bits. Dividimos por 8 para tener el número de bytes = 375.
2 – Como con 3 bits hay 8 posibilidades, asignaremos cada posibilidad a un carácter como:

3a – Lo vimos en el texto CACHE está codificado por 00010000111101.
3b – Leemos los bits de izquierda a derecha, en cuanto la lectura da una letra la escribimos y empezamos a buscar de nuevo en la tabla el carácter correspondiente.
0 no da nada, 00 no da nada, 001 da una B. 1 no da nada, 10 da una A, y así sucesivamente. La última palabra es BADGE.
4a – La longitud sería 1000*3 = 3000 bits.
4b – Para saber la longitud con la tabla de codificación, multiplicaremos para cada carácter su frecuencia por su longitud de codificación: 240*2 + 140*3 + 160*3 + 51*4 + 280*2 + 49*4 + 45* 4 + 35*4. Eso es 2660 bits con una reducción de (3000-2660)/3000 = 11% (que realmente no es terrible...).
5 – Después de realizar el método de Huffman, obtienes el siguiente árbol:

Al final, era la mesa que ya se proporcionaba antes, ¡así que ya era óptima!
